递归神经网络
递归神经网络-RNN简介
循环神经网络与递归神经网络都叫RNN,它们有什么区别呢?
一般来说,神经网络的输入层单元个数是固定的,所以一般用循环或者递归的方式来处理长度可变的输入
循环神经网络:
通过将长度不定的输入分割为等长度的小块,然后再依次的输入到网络中,从而实现了神经网络对变长输入的处理
递归神经网络:
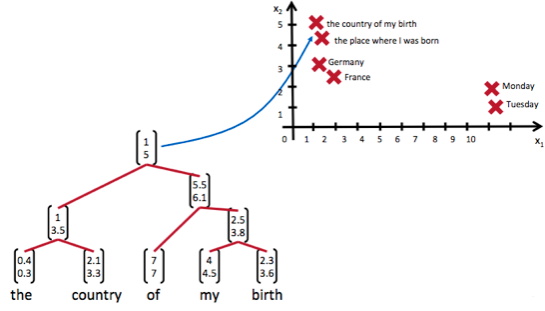
当面对按照树/图结构处理信息更有效的任务时,递归神经网络通常会获得不错的结果。递归神经网络把一个树/图结构信息编码为一个向量,即把信息映射到一个语义向量空间中。这个语义向量空间满足某种性质,比如语义相似的向量距离更近。如下图,递归神经网络将所有的词、句都映射到一个2维向量空间中,也可以是多维空间。句子『the country of my birth』和句子『the place where I was born』的意思是非常接近的,所以表示它们的两个向量在向量空间中的距离很近。
递归神经网络是一种表示学习,它可以将词、句、段、篇按照他们的语义映射到同一个向量空间中,也就是把可组合(树/图结构)的信息表示为一个个有意义的向量。
递归神经网络相比较与循环神经网络其具有更为强大的表示能力,但是在实际应用中并不太流行。其中一个主要原因是,递归神经网络的输入是树/图结构,而这种结构需要花费很多人工去标注。想象一下,如果我们用循环神经网络处理句子,那么我们可以直接把句子作为输入。然而,如果我们用递归神经网络处理句子,我们就必须把每个句子标注为语法解析树的形式,这无疑要花费非常大的精力。很多时候,相对于递归神经网络能够带来的性能提升,这个投入是不太划算的。
递归神经网络-RNN训练算法框架
以处理树型信息为例进行介绍
递归神经网络的前向计算
递归神经网络的输入是两个子节点(也可以是多个),输出就是将这两个子节点编码后产生的父节点,父节点的维度和每个子节点是相同的。
如下图所示,其中,\(c_1\)和\(c_2\)分别是表示两个子节点的向量,即子节点的输出向量。\(p\)是表示父节点的向量,即父节点的输出向量。子节点和父节点组成一个全连接神经网络。我们用矩阵\(W\)表示这些连接上的权重,它的维度将是\(d\times 2d\),其中,\(d\)表示每个节点的维度。父节点的计算公式可以写成,其中tanh是激活函数(也可以用其他的激活函数),\(b\)是偏置项,也是一个维度为d的向量。注意:递归神经网络的权重\(W\)和偏置项\(b\)在所有的节点都是共享的
$$ \mathbf{p} = tanh(W\begin{bmatrix}\mathbf{c}_1\\\mathbf{c}_2\end{bmatrix}+\mathbf{b})\qquad $$
然后,把产生的父节点的向量和其他子节点的向量再次作为网络的输入,再次产生它们的父节点。如此递归下去,直至整棵树处理完毕。最终,将得到的根节点的向量可以认为它是对整棵树的表示,从而实现了把树映射为一个向量,如下图,最终得到向量\(P_3\).
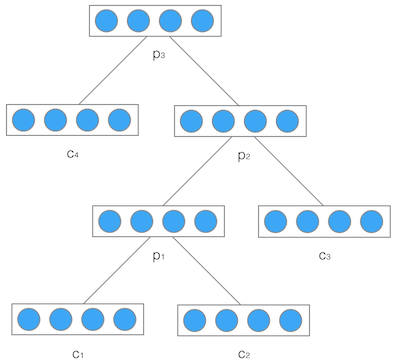
注意:递归神经网络在输入的过程中需要根据输入的树结构依次输入每个子节点。
递归神经网络的反向误差计算
递归神经网络的训练方法和循环神经网络类似,不同之处在于,递归神经网络需要将残差\(\delta\)从根节点反向传播到各个子节点,而循环神经网络将残差\(\delta\)从当前时刻\(t_k\)反向传播到初始时刻\(t_1\)
误差项
将误差从父节点传递到子节点,如下图:
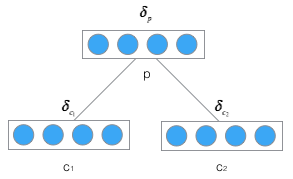
定义\(\delta_p\)将误差函数E相对于父节点p的加权输入\(net_p\)的导数,即:
$$ \delta_p\overset{def}{=}\frac{\partial{E}}{\partial{\mathbf{net}_p}} $$
设\(net_p\)是父节点的加权输入,则,其中\(net_p,c_1,c_2\)都是向量,而\(W\)是矩阵
$$ \mathbf{net}_p=W\begin{bmatrix}\mathbf{c}_1\\\\mathbf{c}_2\end{bmatrix}+\mathbf{b} $$
展开如下图,其中:
- \(p_i\)表示父节点p的第i个分量
- \(c_{1i}\)表示\(c_1\)子节点的第i个分量
- \(c_{2i}\)表示\(c_2\)子节点的第i个分量
- \(w_{p_{i}c_{jk}}\)表示子节点\(c_j\)的第k个分量到父节点p的第i个分量的权重
$$
\begin{align}
\begin{bmatrix}
net_{p_1}\\
net_{p_2}\\
…\\
net_{p_n}
\end{bmatrix}&=
\begin{bmatrix}
w_{p_1c_{11}}&w_{p_1c_{12}}&…&w_{p_1c_{1n}}&w_{p_1c_{21}}&w_{p_1c_{22}}&…&w_{p_1c_{2n}}\\
w_{p_2c_{11}}&w_{p_2c_{12}}&…&w_{p_2c_{1n}}&w_{p_2c_{21}}&w_{p_2c_{22}}&…&w_{p_2c_{2n}}\\
…\\
w_{p_nc_{11}}&w_{p_nc_{12}}&…&w_{p_nc_{1n}}&w_{p_nc_{21}}&w_{p_nc_{22}}&…&w_{p_nc_{2n}}\\
\end{bmatrix}
\begin{bmatrix}
c_{11}\\
c_{12}\\
…\\
c_{1n}\\
c_{21}\\
c_{22}\\
…\\
c_{2n}
\end{bmatrix}\\
&+\begin{bmatrix}
b_1\\
b_2\\
…\\
b_n\\
\end{bmatrix}
\end{align}
$$
根据展开的公式,可以发现,对于子节点\(c_{jk}\)来说,它会影响父节点所有的分量,因此求误差函数\(E\)对\(c_{jk}\)的导数时,必须用到全导数公式,如下,注意:\(\frac{\partial{E}}{\partial{c_{jk}}}\)是一个值
$$
\begin{align}
\frac{\partial{E}}{\partial{c_{jk}}}&=\sum_i{\frac{\partial{E}}{\partial{net_{p_i}}}}\frac{\partial{net_{p_i}}}{\partial{c_{jk}}}\\
&=\sum_i{\delta_{p_i}}w_{p_ic_{jk}}
\end{align}
$$
再把上式变为矩阵形式,从而得到一个向量化表达,这块自己可以看一下,个人觉得实际上就是将数转换为向量
$$ \begin{align} \frac{\partial{E}}{\partial{\mathbf{c}_j}}&=U_j\delta_p \end{align} $$
其中矩阵\(U_j\)是从矩阵\(W\)中提取部分元素组成的矩阵,其单元为:
$$ u_{j_{ik}}=w_{p_kc_{ji}} $$
更加直观的方式如下图:

这个自己可以看一下,子矩阵\(W_1\)和\(W_2\)分别对应子节点\(c_1\)和\(c_2\)到父节点\(p\)的权重,矩阵\(U_j\)为:
$$ U_j=W_j^T $$
现在设\(net_c{j}\)是子节点\(c_j\)的加权输入,\(c_j\)是输出向量,f是子节点c的激活函数,则:
$$
\begin{align}
\mathbf{c}_j=f(\mathbf{net}_{c_j})\\
\end{align}
$$
从而得到
$$
\begin{align}
\delta_{c_j}&=\frac{\partial{E}}{\partial{\mathbf{net}_{c_j}}}\\
&=\frac{\partial{E}}{\partial{\mathbf{c}_j}}\frac{\partial{\mathbf{c}_j}}{\partial{\mathbf{net}_{c_j}}}\\
&=W_j^T\delta_p\circ f’(\mathbf{net}_{c_j})
\end{align}
$$
再将不同子节点\(c_j\)对应的误差项\(\delta_{c_j}\)连接成一个向量\(\delta_c=\begin{bmatrix}\delta_{c_1}\\\ \delta_{c_2}\end{bmatrix}\),从而上式又可以写成,注意: \(net_c\)也是两个子节点的加权输入\(\mathbf{net}_{c_1}\)和\(\mathbf{net}_{c_2}\)连在一起的向量:
$$ \delta_c=W^T\delta_p\circ f’(\mathbf{net}_c)\qquad $$
最后再逐层传递,如下图:
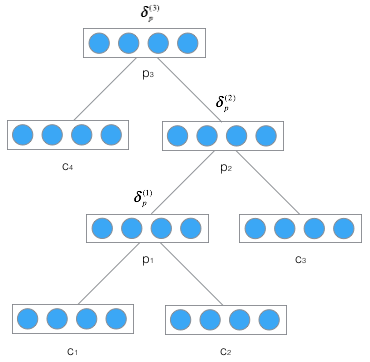
再反复利用上式,在已知\(\delta_p^{(3)}\)的情况下,可以传递算出\(\delta_p^{(1)}\)。**注意:\(\delta^{(2)}=\begin{bmatrix}\delta_c^{(2)}\\\ \delta_p^{(2)}\end{bmatrix}\),\([\delta^{(2)}]_p\)表示向量\(\delta^{(2)}\)属于节点p的部分 **
$$
\begin{align}
\delta^{(2)}&=W^T\delta_p^{(3)}\circ f’(\mathbf{net}^{(2)})\\
\delta_p^{(2)}&=[\delta^{(2)}]_p\\
\delta^{(1)}&=W^T\delta_p^{(2)}\circ f’(\mathbf{net}^{(1)})\\
\delta_p^{(1)}&=[\delta^{(1)}]_p\\
\end{align}
$$
权重梯度的计算
根据加权输入的计算公式,其中\(\mathbf{net}_p^{(l)}\)表示第l层的父节点的加权输入,\(\mathbf{c}^{(l)}\)表示第l层的子节点,\(W\)是权重矩阵,\(b\)是偏置项
$$ \mathbf{net}_p^{(l)}=W\mathbf{c}^{(l)}+\mathbf{b} $$
然后可以求得误差函数在第l层对权重的梯度:
$$
\begin{align}
\frac{\partial{E}}{\partial{w_{ji}^{(l)}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{p_j}^{(l)}}}\frac{\partial{\mathbf{net}_{p_j}^{(l)}}}{\partial{w_{ji}^{(l)}}}\\
&=\delta_{p_j}^{(l)}c_i^{(l)}\\
\end{align}
$$
上式是针对一个权重项\(w_{ji}\)的公式,现在需要把它扩展为对所有的权重项的公式。我们可以把上式写成矩阵的形式(在下面的公式中,m=2n):
$$
\begin{align}
\frac{\partial{E}}{\partial{W^{(l)}}}&=
\begin{bmatrix}
\frac{\partial{E}}{\partial{w_{11}^{(l)}}}&
\frac{\partial{E}}{\partial{w_{12}^{(l)}}}&
…&
\frac{\partial{E}}{\partial{w_{1m}^{(l)}}}\\
\frac{\partial{E}}{\partial{w_{21}^{(l)}}}&
\frac{\partial{E}}{\partial{w_{22}^{(l)}}}&
…&
\frac{\partial{E}}{\partial{w_{2m}^{(l)}}}\\
…\\\
\frac{\partial{E}}{\partial{w_{n1}^{(l)}}}&
\frac{\partial{E}}{\partial{w_{n2}^{(l)}}}&
…&
\frac{\partial{E}}{\partial{w_{nm}^{(l)}}}\\
\end{bmatrix}\\
&=
\begin{bmatrix}
\delta_{p_1}^{(l)}c_1^l&\delta_{p_1}^{(l)}c_2^l&…&\delta_{p_1}^lc_m^{(l)}\\
\delta_{p_2}^{(l)}c_1^l&\delta_{p_2}^{(l)}c_2^l&…&\delta_{p_2}^lc_m^{(l)}\\
…\\\
\delta_{p_n}^{(l)}c_1^l&\delta_{p_n}^{(l)}lc_2^l&…&\delta_{p_n}^lc_m^{(l)}\\
\end{bmatrix}
&=\delta^{{(l)}}(\mathbf{c}^{(l)})^T\qquad
\end{align}
$$
由于权重\(W\)是在所有层共享的,因此递归神经网络最终的权重梯度是各个层权重梯度之和。即:
$$ \frac{\partial{E}}{\partial{W}}=\sum_l\frac{\partial{E}}{\partial{W^{(l)}}}\qquad $$
偏置\(b\)的偏置项之和方法与求权重梯度一样,本文不再继续推导
权重更新
利用梯度下降优化算法,权重的更新公式和偏置项的更新公式如下,其中\(\eta\)是学习速率常数
$$
W\gets W + \eta\frac{\partial{E}}{\partial{W}}\\
\mathbf{b}\gets \mathbf{b} + \eta\frac{\partial{E}}{\partial{\mathbf{b}}}
$$
递归神经网络的应用
递归神经网络完成句子的语法分析并产生一个语法解析树,如下图所示:
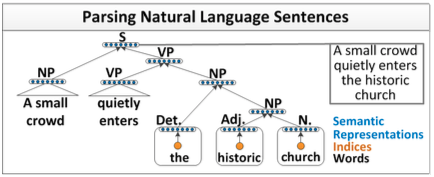
将一句话输入到神经网络中,然后神经网络返回一个解析树。为了做到这一点,我们需要给神经网络再加上一层,负责打分。分数越高,说明两个子节点结合更加紧密,分数越低,说明两个子节点结合更松散。如下图所示:
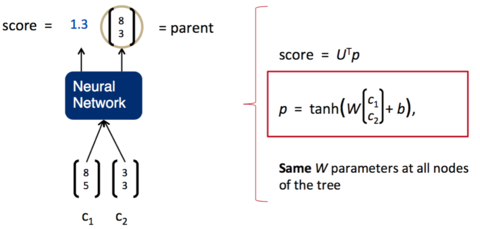
一旦这个打分函数训练好了(也就是矩阵U的各项值变为合适的值),我们就可以利用贪心算法来实现句子的解析。举例如下:
- 先将词按照顺序两两输入神经网络,得到第一组打分
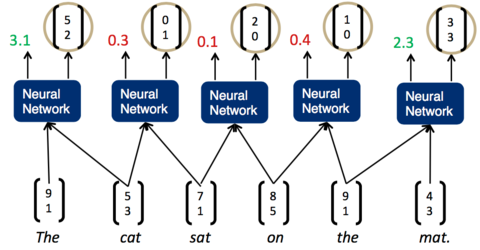
- 现在分数最高的是第一组,The cat,说明它们的结合是最紧密的。这样,我们可以先将它们组合为一个节点。然后,再次两两计算相邻子节点的打分
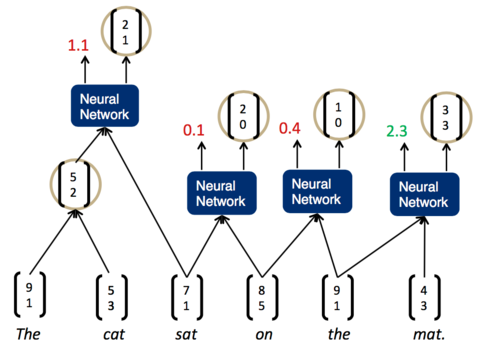
- 现在,分数最高的是最后一组,the mat。于是,我们将它们组合为一个节点,再两两计算相邻节点的打分
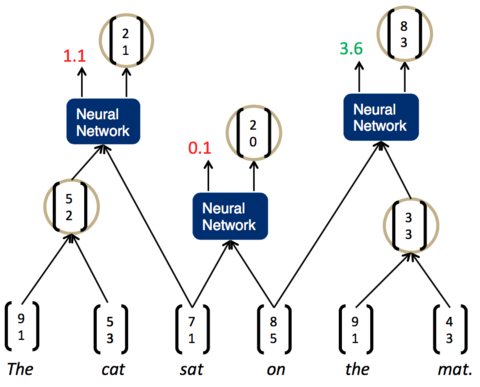
- 这时,我们发现最高的分数是on the mat,把它们组合为一个节点,继续两两计算相邻节点的打分……最终,我们就能够得到整个解析树
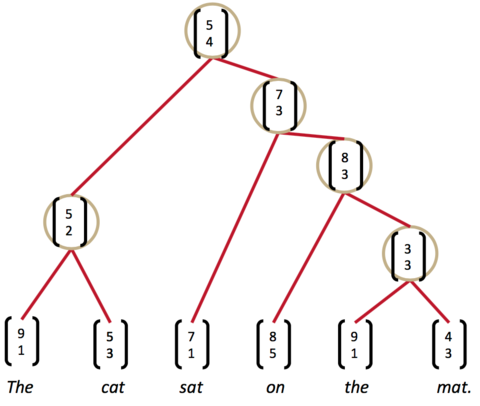
对于打分函数score,需要定义一个目标函数。这里使用Max-Margin目标函数,定义如下,下式中,\(x_i,y_i\)分别表示是第i个训练样本的输入和标签,注意:标签\(y_i\)是一个解析树,\(s(x_i,y_i)\)是打分函数,是对第i个训练样本的打分。因为训练样本的标签肯定是正确的,我们希望s对它的打分越高越好,即\(s(x_i,y_i)\)分数越高越好。\(A(x_1)\)是所有可能的解析树的集合,\(s(x_i,y)\)是对某个可能的解析树y的打分。\(\Delta(y,y_i)\)是对错误的惩罚,也就是说,如果某个解析树\(y\)和标签\(y_i\)是一样的,那么\(\Delta(y,y_i)\)为0,如果网络的输出错的越离谱,那么\(\Delta(y,y_i)\)的值就越大。\(max(s(x_i,y)+\Delta(y,y_i))\)表示在所有解析树里的最高分。\(\Delta(y,y_i)\)相当于Margin,即虽然希望打分函数s对正确的树打分比对错误的树打分高,但也不要高过Margin的值。
$$ J(\theta)=max(0, \sum_i\underset{y\in A(x_i)}{max}(s(x_i,y)+\Delta(y,y_i))-s(x_i,y_i)) $$
最后优化\(\theta\),使目标函数取最小值,即
$$ \theta=\underset{\theta}{argmin}J(\theta) $$
下式是对惩罚函数\(\Delta(y,y_i)\)的定义,\(N(y)\)是树y节点的集合;subTree(d)是以d为节点的子树。
$$ \Delta(y,y_i)=k\sum_{d\in N(y)}\mathbf{1}{{subTree(d)\notin y_i}} $$
上式的含义是:如果以d为节点的子树没有出现在标签\(y_i\)中,那么函数值+1。最终,惩罚函数的值,是树y中没有出现在树中的子树的个数,再乘上一个系数k。其实也就是关于两棵树差异的一个度量。
\(s(x,y)\)是对一个样本最终的打分,它是对树y每个节点打分的总和:
$$ s(x,y)=\sum_{n\in nodes(y)}s_n $$
本文主要参考了零基础入门深度学习-递归神经网络