LSTM
LSTM简介
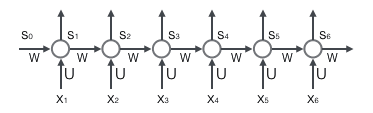
为了应对RNN梯度消失和梯度爆炸的问题,后面提出了LSTM网络,RNN网络结构图如下,RNN的隐藏层只有一个状态:
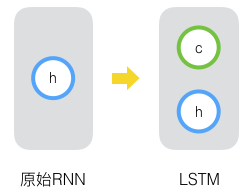
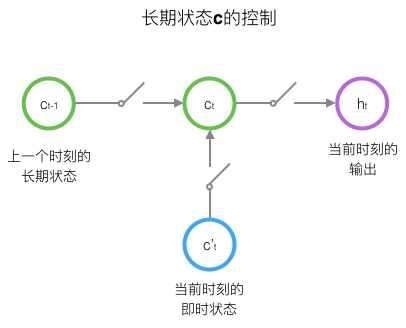
LSTM相比较与RNN再增加了一个状态c,通过状态c来保存长期的状态,新增加的状态c称为单元状态,如下图:
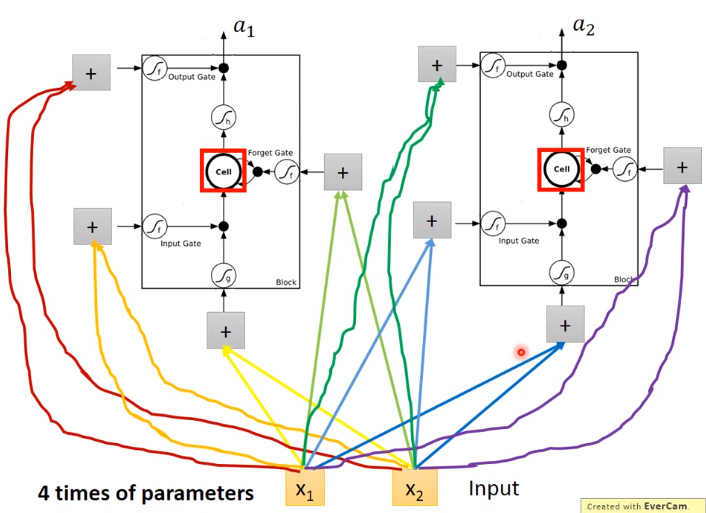
LSTM使用三个控制开关控制长期状态c,如下图:
- 负责控制继续保存上一个时刻的长期状态c
- 负责控制把当前时刻的即时状态输入到长期状态c
- 负责控制长期状态c控制LSTM的当前输出
LSTM训练算法框架
LSTM的前向计算
LSTM使用到了门的概念,门实际上就是一层全连接层,它的输入是一个向量,输出是一个0-1之间的实数向量,假设W是门的权重向量,b是b偏置项,\(\sigma\)(也就是sigmoid函数)的值域是(0,1),门就可以表示为: $$ g(\mathbf{x})=\sigma(W\mathbf{x}+\mathbf{b}) $$
LSTM使用两个门来控制单元状态c的内容:
- 遗忘门(forget gate),它决定了上一时刻的单元状态\(\mathbf{c}_{t-1}\)有多少保留到当期时刻\(\mathbf{c}_{t}\)
- 输入门(input gate),它决定了当前时刻网络的输入\(\mathbf{x}_{t}\)有多少保存到单元状态\(\mathbf{c}_{t}\)
LSTM使用一个门来控制单元状态到LSTM的当前输出
- LSTM用输出门(output gate)来控制单元状态\(\mathbf{c}_{t}\)有多少输出到LSTM的当前输出值\(\mathbf{h}_{t}\)
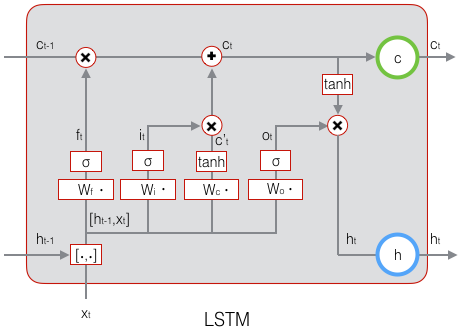
下图是LSTM的细节图:
一. 遗忘门
下式中\(W_f\)是遗忘门的权重矩阵,\([\mathbf{h}_{t-1},\mathbf{x}_t]\)表示把两个向量连接成一个更长的向量,\(\mathbf{b}_f\)是遗忘门的偏置项,\(\sigma\)是sigmoid函数,如果输入的维度是\(d_x\),隐藏层的维度是\(d_h\),单元状态的维度是\(d_c\)(通常\(d_c=d_h\)),则遗忘门的权重矩阵\(W_f\)维度是\(d_c\times (d_h+d_x)\)
$$ \mathbf{f}_t=\sigma(W_f\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_f)\qquad\quad $$
其中\(W_f\)实际上是由两个矩阵拼接而成的,一个是\(W_{fh}\),它对应着输入项\(h_{t-1}\),其维度为\(d_c\times d_h\)。另一个是\(W_{fx}\),它对应着输入项\(X_t\),其维度为\(d_c\times d_x\),\(W_f\)可以写为:
$$
\begin{align}
\begin{bmatrix}W_f\end{bmatrix}\begin{bmatrix}\mathbf{h}_{t-1}\\
\mathbf{x}_t\end{bmatrix}&=
\begin{bmatrix}W_{fh}&W_{fx}\end{bmatrix}\begin{bmatrix}\mathbf{h}_{t-1}\\
\mathbf{x}_t\end{bmatrix}\\
&=W_{fh}\mathbf{h}_{t-1}+W_{fx}\mathbf{x}_t
\end{align}
$$
二. 输入门
下式中,\(W_i\)是输入门的权重矩阵,\(b_i\)是输入门的偏置项
$$ \mathbf{i}_t=\sigma(W_i\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_i)\qquad\quad $$
三. 当前时刻的单元状态\(\mathbf{c}_t\)
- 计算用于描述当前输入的单元状态\(\mathbf{\tilde{c}}_t\),它是根据上一次的输出和本次输入来计算的:
$$ \mathbf{\tilde{c}}_t=\tanh(W_c\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_c)\qquad\quad $$
- 计算当前时刻的单元状态\(\mathbf{c}_t\),它是由上一次的单元状态\(\mathbf{c}_{t-1}\)按元素乘以遗忘门\(\mathbf{f}_t\),再用当前输入的单元状态\(\mathbf{\tilde{c}}_t\)按元素乘以输入门\(i_t\),再将两个积加和产生的,符号\(\circ\)表示按元素乘。这样,我们就把LSTM关于当前的记忆\(\mathbf{\tilde{c}}_t\)和长期的记忆\(\mathbf{c}_{t-1}\)组合在一起,形成了新的单元状态\(\mathbf{c}_{t}\)。通过遗忘门的控制,可以保存很久很久之前的信息,通过输入门的控制,又可以避免当前无关紧要的内容进入记忆。
$$ \mathbf{c}_t=f_t\circ{\mathbf{c}_{t-1}}+i_t\circ{\mathbf{\tilde{c}}_t}\qquad\quad $$
四. 输出门
$$ \mathbf{o}_t=\sigma(W_o\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_o)\qquad\quad $$
五. LSTM最终的输出
LSTM最终的输出是由输出门和单元状态共同决定的:
$$ \mathbf{h}_t=\mathbf{o}_t\circ \tanh(\mathbf{c}_t)\qquad\quad $$
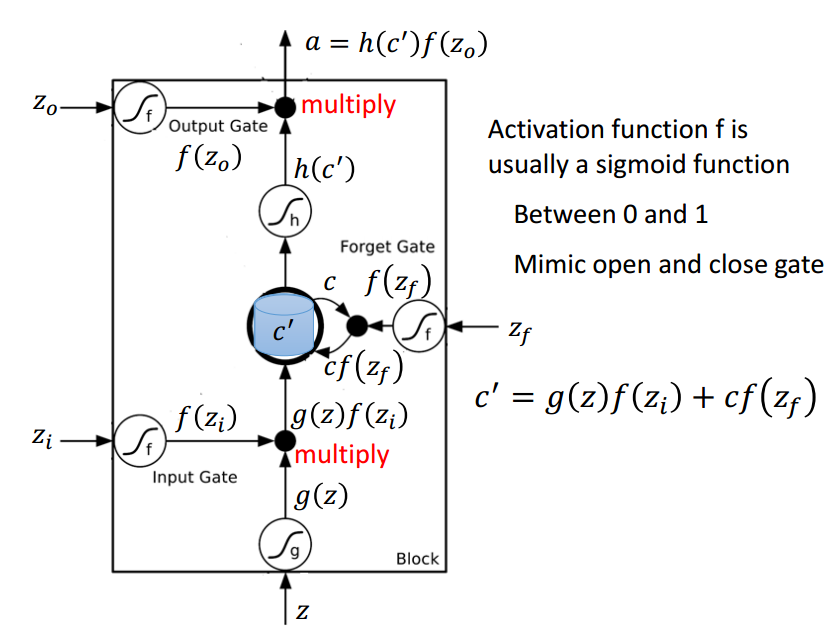
更加直观的图如下图,下图更易于理解LSTM,举例下图只是说明下图理解LSTM更加直观,公式的推导还是使用上图的LSTM的例子。
LSTM的反向误差计算
LSTM误差项的反向传播包括两个方向:
- 沿时间的反向传播,即从当前t时刻开始,计算每个时刻的误差项
- 将误差项向上一层传播
公式和符号说明
设定门的激活函数是sigmoid函数,输出的激活函数为tanh函数,它们的导数分别如下,只要计算出原函数的值,那么就可以用它来计算出导数的值:
$$
\begin{align}
\sigma(z)&=y=\frac{1}{1+e^{-z}}\\
\sigma’(z)&=y(1-y)\\
\tanh(z)&=y=\frac{e^z-e^{-z}}{e^z+e^{-z}}\\
\tanh’(z)&=1-y^2
\end{align}
$$
LSTM需要学习的参数共有4组:
- 遗忘门的权重矩阵\(W_f\)和偏置项\(b_f\)
- 输入门的权重矩阵\(W_i\)和偏置项\(b_i\)
- 输出门的权重矩阵\(W_o\)和偏置项\(b_o\)
- 单元状态的权重矩阵\(W_c\)和偏置项\(b_c\)
由于权重矩阵在反向传播中有两个方向,因此在后续的推导中,权重矩阵\(W_f\),\(W_i\),\(W_c\),\(W_o\)都被分为两个矩阵:\(W_{fh}\),\(W_{fx}\),\(W_{ih}\),\(W_{ix}\),\(W_{oh}\),\(W_{ox}\),\(W_{ch}\),\(W_{cx}\)。
\(\circ\)符号作用于两个向量时,运算如下,注意\(\mathbf{a}\)表示列向量:
$$ \mathbf{a}\circ\mathbf{b}=\begin{bmatrix} a_1\\\ a_2\\\ a_3\\\ …\\\ a_n \end{bmatrix}\circ\begin{bmatrix} b_1\\\ b_2\\\ b_3\\\ …\\\ b_n \end{bmatrix}=\begin{bmatrix} a_1b_1\\\ a_2b_2\\\ a_3b_3\\\ …\\\ a_nb_n \end{bmatrix} $$
当\(\circ\)符号作用于一个向量和一个矩阵时,运算如下:
$$
\begin{align}
\mathbf{a}\circ X&=\begin{bmatrix}
a_1\\\ a_2\\\ a_3\\\ …\\\ a_n
\end{bmatrix}\circ\begin{bmatrix}
x_{11} & x_{12} & x_{13} & … & x_{1n}\\
x_{21} & x_{22} & x_{23} & … & x_{2n}\\
x_{31} & x_{32} & x_{33} & … & x_{3n}\\
& & …\\
x_{n1} & x_{n2} & x_{n3} & … & x_{nn}\\
\end{bmatrix}\\
&=\begin{bmatrix}
a_1x_{11} & a_1x_{12} & a_1x_{13} & … & a_1x_{1n}\\
a_2x_{21} & a_2x_{22} & a_2x_{23} & … & a_2x_{2n}\\
a_3x_{31} & a_3x_{32} & a_3x_{33} & … & a_3x_{3n}\\
& & …\\
a_nx_{n1} & a_nx_{n2} & a_nx_{n3} & … & a_nx_{nn}\\
\end{bmatrix}
\end{align}
$$
当\(\circ\)符号作用于两个矩阵时,两个矩阵对对应位置的元素相乘。
两个矩阵相乘时,有如下两个特例:
- 当一个对角矩阵右乘一个矩阵时,相当于用对角矩阵的对角线组成的向量按元素右乘一个矩阵:
$$ diag[\mathbf{a}]X=\mathbf{a}\circ X $$
- 当一个行向量右乘一个对角矩阵时,相当于这个行向量按元素右乘右边矩阵对角线组成的向量,注意:下式的\(\mathbf{a}\circ\mathbf{b}\)是一个1*5的矩阵
$$ \mathbf{a}^Tdiag[\mathbf{b}]=\mathbf{a}\circ\mathbf{b} $$
其余使用到的公式如下:
$$
\begin{align}
\mathbf{net}_{f,t}&=W_f[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_f\\
&=W_{fh}\mathbf{h}_{t-1}+W_{fx}\mathbf{x}_t+\mathbf{b}_f\\
\mathbf{net}_{i,t}&=W_i[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_i\\
&=W_{ih}\mathbf{h}_{t-1}+W_{ix}\mathbf{x}_t+\mathbf{b}_i\\
\mathbf{net}_{\tilde{c},t}&=W_c[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_c\\
&=W_{ch}\mathbf{h}_{t-1}+W_{cx}\mathbf{x}_t+\mathbf{b}_c\\
\mathbf{net}_{o,t}&=W_o[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_o\\
&=W_{oh}\mathbf{h}_{t-1}+W_{ox}\mathbf{x}_t+\mathbf{b}_o\\
\delta_{f,t}&\overset{def}{=}\frac{\partial{E}}{\partial{\mathbf{net}_{f,t}}}\\
\delta_{i,t}&\overset{def}{=}\frac{\partial{E}}{\partial{\mathbf{net}_{i,t}}}\\
\delta_{\tilde{c},t}&\overset{def}{=}\frac{\partial{E}}{\partial{\mathbf{net}_{\tilde{c},t}}}\\
\delta_{o,t}&\overset{def}{=}\frac{\partial{E}}{\partial{\mathbf{net}_{o,t}}}\\
\end{align}
$$
误差项
在t时刻,LSTM的输出值为\(\mathbf{h}_t\)。在LSTM中定义t时刻的误差项\(\delta_t\)为:
$$ \delta_t\overset{def}{=}\frac{\partial{E}}{\partial{\mathbf{h}_t}} $$
注意
这里误差项是损失函数对输出值的导数,并不是损失函数对加权输入\(net_t^l\)的导数
为什么???
因为LSTM有四个加权输入,分别对应\(f_t\),\(i_t\),\(c_t\),\(o_t\),从数学公式推导上,希望往上一时刻传递的误差项是一个并不是四个,不能通过简单的对四个加权输入相加来类比于误差项。
误差项沿时间的反向传递
沿时间反向传递误差项,需要计算出t-1时刻的误差项\(\delta_{t-1}\)
$$
\begin{align}
\delta_{t-1}^T&=\frac{\partial{E}}{\partial{\mathbf{h_{t-1}}}}\\
&=\frac{\partial{E}}{\partial{\mathbf{h_t}}}\frac{\partial{\mathbf{h_t}}}{\partial{\mathbf{h_{t-1}}}}\\
&=\delta_{t}^T\frac{\partial{\mathbf{h_t}}}{\partial{\mathbf{h_{t-1}}}}
\end{align}
$$
类似于之前的求RNN的方法,根据\(\mathbf{h}_t\)的计算公式,即前向计算的:
$$
\begin{align}
\mathbf{h}_t&=\mathbf{o}_t\circ \tanh(\mathbf{c}_t)\\
\mathbf{c}_t&=\mathbf{f}_t\circ\mathbf{c}_{t-1}+\mathbf{i}_t\circ\mathbf{\tilde{c}}_t
\end{align}
$$
再根据前向计算的公式,显然得到\(\mathbf{o}_t\),\(\mathbf{f}_t\),\(\mathbf{}_t\),\(\mathbf{\tilde{c}}_t\)都是\(\mathbf{h}_{t-1}\)的函数:
$$ \mathbf{o}_t=\sigma(W_o\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_o)\qquad\quad $$
$$ \mathbf{f}_t=\sigma(W_f\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_f)\qquad\quad $$
$$ \mathbf{i}_t=\sigma(W_i\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_i)\qquad\quad $$
$$ \mathbf{\tilde{c}}_t=\tanh(W_c\cdot[\mathbf{h}_{t-1},\mathbf{x}_t]+\mathbf{b}_c)\qquad\quad $$
利用全导数公式可得:
$$
\begin{align}
\delta_t^T\frac{\partial{\mathbf{h_t}}}{\partial{\mathbf{h_{t-1}}}}&=\delta_t^T\frac{\partial{\mathbf{h_t}}}{\partial{\mathbf{o}_t}}\frac{\partial{\mathbf{o}_t}}{\partial{\mathbf{net}_{o,t}}}\frac{\partial{\mathbf{net}_{o,t}}}{\partial{\mathbf{h_{t-1}}}}\\
&+\delta_t^T\frac{\partial{\mathbf{h_t}}}{\partial{\mathbf{c}_t}}\frac{\partial{\mathbf{c}_t}}{\partial{\mathbf{f_{t}}}}\frac{\partial{\mathbf{f}_t}}{\partial{\mathbf{net}_{f,t}}}\frac{\partial{\mathbf{net}_{f,t}}}{\partial{\mathbf{h_{t-1}}}}\\
&+\delta_t^T\frac{\partial{\mathbf{h_t}}}{\partial{\mathbf{c}_t}}\frac{\partial{\mathbf{c}_t}}{\partial{\mathbf{i_{t}}}}\frac{\partial{\mathbf{i}_t}}{\partial{\mathbf{net}_{i,t}}}\frac{\partial{\mathbf{net}_{i,t}}}{\partial{\mathbf{h_{t-1}}}}\\
&+\delta_t^T\frac{\partial{\mathbf{h_t}}}{\partial{\mathbf{c}_t}}\frac{\partial{\mathbf{c}_t}}{\partial{\mathbf{\tilde{c}}_{t}}}\frac{\partial{\mathbf{\tilde{c}}_t}}{\partial{\mathbf{net}_{\tilde{c},t}}}\frac{\partial{\mathbf{net}_{\tilde{c},t}}}{\partial{\mathbf{h_{t-1}}}}\\
&=\delta_{o,t}^T\frac{\partial{\mathbf{net}_{o,t}}}{\partial{\mathbf{h_{t-1}}}}
+\delta_{f,t}^T\frac{\partial{\mathbf{net}_{f,t}}}{\partial{\mathbf{h_{t-1}}}}
+\delta_{i,t}^T\frac{\partial{\mathbf{net}_{i,t}}}{\partial{\mathbf{h_{t-1}}}}
+\delta_{\tilde{c},t}^T\frac{\partial{\mathbf{net}_{\tilde{c},t}}}{\partial{\mathbf{h_{t-1}}}}\qquad\quad
\end{align}
$$
根据上式中tanh()的求导公式,行向量乘以矩阵的计算:
$$
\begin{align}
\tanh(z)&=y\\
\tanh’(z)&=1-y^2
\end{align}
$$
$$ \mathbf{a}^Tdiag[\mathbf{b}]=\mathbf{a}\circ\mathbf{b} $$
可以求出:
$$
\begin{align}
\frac{\partial{\mathbf{h_t}}}{\partial{\mathbf{o}_t}}&=diag[\tanh(\mathbf{c}_t)]\\
\frac{\partial{\mathbf{h_t}}}{\partial{\mathbf{c}_t}}&=diag[\mathbf{o}_t\circ(1-\tanh(\mathbf{c}_t)^2)]
\end{align}
$$
$$
\begin{align}
\frac{\partial{\mathbf{c}_t}}{\partial{\mathbf{f_{t}}}}&=diag[\mathbf{c}_{t-1}]\\
\frac{\partial{\mathbf{c}_t}}{\partial{\mathbf{i_{t}}}}&=diag[\mathbf{\tilde{c}}_t]\\
\frac{\partial{\mathbf{c}_t}}{\partial{\mathbf{\tilde{c}_{t}}}}&=diag[\mathbf{i}_t]\\
\end{align}
$$
又因为:
$$
\begin{align}
\mathbf{o}_t&=\sigma(\mathbf{net}_{o,t})\\
\mathbf{net}_{o,t}&=W_{oh}\mathbf{h}_{t-1}+W_{ox}\mathbf{x}_t+\mathbf{b}_o\\\
\mathbf{f}_t&=\sigma(\mathbf{net}_{f,t})\\
\mathbf{net}_{f,t}&=W_{fh}\mathbf{h}_{t-1}+W_{fx}\mathbf{x}_t+\mathbf{b}_f\\\
\mathbf{i}_t&=\sigma(\mathbf{net}_{i,t})\\
\mathbf{net}_{i,t}&=W_{ih}\mathbf{h}_{t-1}+W_{ix}\mathbf{x}_t+\mathbf{b}_i\\\
\mathbf{\tilde{c}}_t&=\tanh(\mathbf{net}_{\tilde{c},t})\\
\mathbf{net}_{\tilde{c},t}&=W_{ch}\mathbf{h}_{t-1}+W_{cx}\mathbf{x}_t+\mathbf{b}_c\\
\end{align}
$$
容易得出:
$$
\begin{align}
\frac{\partial{\mathbf{o}_t}}{\partial{\mathbf{net}_{o,t}}}&=diag[\mathbf{o}_t\circ(1-\mathbf{o}_t)]\\
\frac{\partial{\mathbf{net}_{o,t}}}{\partial{\mathbf{h_{t-1}}}}&=W_{oh}\\
\frac{\partial{\mathbf{f}_t}}{\partial{\mathbf{net}_{f,t}}}&=diag[\mathbf{f}_t\circ(1-\mathbf{f}_t)]\\
\frac{\partial{\mathbf{net}_{f,t}}}{\partial{\mathbf{h}_{t-1}}}&=W_{fh}\\
\frac{\partial{\mathbf{i}_t}}{\partial{\mathbf{net}_{i,t}}}&=diag[\mathbf{i}_t\circ(1-\mathbf{i}_t)]\\
\frac{\partial{\mathbf{net}_{i,t}}}{\partial{\mathbf{h}_{t-1}}}&=W_{ih}\\
\frac{\partial{\mathbf{\tilde{c}}_t}}{\partial{\mathbf{net}_{\tilde{c},t}}}&=diag[1-\mathbf{\tilde{c}}_t^2]\\
\frac{\partial{\mathbf{net}_{\tilde{c},t}}}{\partial{\mathbf{h}_{t-1}}}&=W_{ch}
\end{align}
$$
将上述偏导数带入全导数公式,可得:
$$
\begin{align}
\delta_{t-1}&=\delta_{o,t}^T\frac{\partial{\mathbf{net}_{o,t}}}{\partial{\mathbf{h_{t-1}}}}
+\delta_{f,t}^T\frac{\partial{\mathbf{net}_{f,t}}}{\partial{\mathbf{h_{t-1}}}}
+\delta_{i,t}^T\frac{\partial{\mathbf{net}_{i,t}}}{\partial{\mathbf{h_{t-1}}}}
+\delta_{\tilde{c},t}^T\frac{\partial{\mathbf{net}_{\tilde{c},t}}}{\partial{\mathbf{h_{t-1}}}}\\
&=\delta_{o,t}^T W_{oh}
+\delta_{f,t}^TW_{fh}
+\delta_{i,t}^TW_{ih}
+\delta_{\tilde{c},t}^TW_{ch}\qquad\quad\\
\end{align}
$$
根据:
$$ \delta_{o,t}^T = \frac{\partial E}{\partial h_t}\frac{\partial h_t}{\partial o_t}\frac{\partial o_t}{\partial net_{o,t}} $$
其余类似于上式,可知:
$$
\begin{align}
\delta_{o,t}^T&=\delta_t^T\circ\tanh(\mathbf{c}_t)\circ\mathbf{o}_t\circ(1-\mathbf{o}_t)\qquad\quad\\
\delta_{f,t}^T&=\delta_t^T\circ\mathbf{o}_t\circ(1-\tanh(\mathbf{c}_t)^2)\circ\mathbf{c}_{t-1}\circ\mathbf{f}_t\circ(1-\mathbf{f}_t)\qquad\\
\delta_{i,t}^T&=\delta_t^T\circ\mathbf{o}_t\circ(1-\tanh(\mathbf{c}_t)^2)\circ\mathbf{\tilde{c}}_t\circ\mathbf{i}_t\circ(1-\mathbf{i}_t)\qquad\quad\\
\delta_{\tilde{c},t}^T&=\delta_t^T\circ\mathbf{o}_t\circ(1-\tanh(\mathbf{c}_t)^2)\circ\mathbf{i}_t\circ(1-\mathbf{\tilde{c}}^2)\qquad\quad
\end{align}
$$
类似于上文RNN的方法,最后可以写出将误差项向前传递到任意k时刻的公式:
$$ \delta_k^T=\prod_{j=k}^{t-1}\delta_{o,j}^TW_{oh} +\delta_{f,j}^TW_{fh} +\delta_{i,j}^TW_{ih} +\delta_{\tilde{c},j}^TW_{ch}\qquad\quad $$
误差项传递到上一层的反向传递
假设当前为第l层,定义l-1层的误差项是误差函数对l-1层加权输入的导数,即:
$$ \delta_t^{l-1}\overset{def}{=}\frac{\partial{E}}{\mathbf{net}_t^{l-1}} $$
抽象来看,本次四种用到的加权输入可以看做一个加权输入,即本次LSTM的输入\(x_t\)由下面的公式计算,其中\(f^{l-1}\)表示第l-1层的激活函数:
$$ \mathbf{x}_t^l=f^{l-1}(\mathbf{net}_t^{l-1}) $$
因为\(\mathbf{net}_{f,t}^l,\mathbf{net}_{i,t}^l,\mathbf{net}_{\tilde{c},t}^l,\mathbf{net}_{o,t}^l\)都是\(x_t\)的函数,\(x_t\)又是\(\mathbf{net}_t^{l-1}\)的函数,因此,要求出损失函数对\(\mathbf{net}_t^{l-1}\)的导数,就需要使用全导数公式:
$$
\begin{align}
\frac{\partial{E}}{\partial{\mathbf{net}_t^{l-1}}}&=\frac{\partial{E}}{\partial{\mathbf{\mathbf{net}_{f,t}^l}}}\frac{\partial{\mathbf{\mathbf{net}_{f,t}^l}}}{\partial{\mathbf{x}_t^l}}\frac{\partial{\mathbf{x}_t^l}}{\partial{\mathbf{\mathbf{net}_t^{l-1}}}}\\
&+\frac{\partial{E}}{\partial{\mathbf{\mathbf{net}_{i,t}^l}}}\frac{\partial{\mathbf{\mathbf{net}_{i,t}^l}}}{\partial{\mathbf{x}_t^l}}\frac{\partial{\mathbf{x}_t^l}}{\partial{\mathbf{\mathbf{net}_t^{l-1}}}}\\
&+\frac{\partial{E}}{\partial{\mathbf{\mathbf{net}_{\tilde{c},t}^l}}}\frac{\partial{\mathbf{\mathbf{net}_{\tilde{c},t}^l}}}{\partial{\mathbf{x}_t^l}}\frac{\partial{\mathbf{x}_t^l}}{\partial{\mathbf{\mathbf{net}_t^{l-1}}}}\\
&+\frac{\partial{E}}{\partial{\mathbf{\mathbf{net}_{o,t}^l}}}\frac{\partial{\mathbf{\mathbf{net}_{o,t}^l}}}{\partial{\mathbf{x}_t^l}}\frac{\partial{\mathbf{x}_t^l}}{\partial{\mathbf{\mathbf{net}_t^{l-1}}}}\\
&=\delta_{f,t}^TW_{fx}\circ f’(\mathbf{net}_t^{l-1})+\delta_{i,t}^TW_{ix}\circ f’(\mathbf{net}_t^{l-1})\\
&+\delta_{\tilde{c},t}^TW_{cx}\circ f’(\mathbf{net}_t^{l-1})+\delta_{o,t}^TW_{ox}\circ f’(\mathbf{net}_t^{l-1})\\
&=(\delta_{f,t}^TW_{fx}+\delta_{i,t}^TW_{ix}+\delta_{\tilde{c},t}^TW_{cx}+\delta_{o,t}^TW_{ox})\circ f’(\mathbf{net}_t^{l-1})
\end{align}
$$
权重梯度的计算
对于\(W_{fh}\),\(W_{ih}\),\(W_{ch}\),\(W_{oh}\)的权重梯度,根据上一篇RNN的介绍,知道它的梯度是各个时刻梯度之和,因此首先求出在t时刻的梯度,然后再求出最终的梯度。
上文已经求得了误差项\(\delta_{o,t}\),\(\delta_{f,t}\),\(\delta_{i,t}\),\(\delta_{\tilde{c},t}\),因此很容易求出t时刻的\(W_{fh}\),\(W_{ih}\),\(W_{ch}\),\(W_{oh}\)的权重梯度。
$$
\begin{align}
\frac{\partial{E}}{\partial{W_{oh,t}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{o,t}}}\frac{\partial{\mathbf{net}_{o,t}}}{\partial{W_{oh,t}}}\\
&=\delta_{o,t}\mathbf{h}_{t-1}^T\\\
\frac{\partial{E}}{\partial{W_{fh,t}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{f,t}}}\frac{\partial{\mathbf{net}_{f,t}}}{\partial{W_{fh,t}}}\\
&=\delta_{f,t}\mathbf{h}_{t-1}^T\\\
\frac{\partial{E}}{\partial{W_{ih,t}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{i,t}}}\frac{\partial{\mathbf{net}_{i,t}}}{\partial{W_{ih,t}}}\\
&=\delta_{i,t}\mathbf{h}_{t-1}^T\\\
\frac{\partial{E}}{\partial{W_{ch,t}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{\tilde{c},t}}}\frac{\partial{\mathbf{net}_{\tilde{c},t}}}{\partial{W_{ch,t}}}\\
&=\delta_{\tilde{c},t}\mathbf{h}_{t-1}^T\\
\end{align}
$$
将各个时刻的梯度加在一起,就能得到最终的梯度:
$$
\begin{align}
\frac{\partial{E}}{\partial{W_{oh}}}&=\sum_{j=1}^t\delta_{o,j}\mathbf{h}_{j-1}^T\\
\frac{\partial{E}}{\partial{W_{fh}}}&=\sum_{j=1}^t\delta_{f,j}\mathbf{h}_{j-1}^T\\
\frac{\partial{E}}{\partial{W_{ih}}}&=\sum_{j=1}^t\delta_{i,j}\mathbf{h}_{j-1}^T\\
\frac{\partial{E}}{\partial{W_{ch}}}&=\sum_{j=1}^t\delta_{\tilde{c},j}\mathbf{h}_{j-1}^T\\
\end{align}
$$
对偏置项\(b_f,b_i,b_c,b_o\)的梯度,也是将各个时刻的梯度加在一起。下面是各个时刻的偏置项梯度:
$$
\begin{align}
\frac{\partial{E}}{\partial{\mathbf{b}_{o,t}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{o,t}}}\frac{\partial{\mathbf{net}_{o,t}}}{\partial{\mathbf{b}_{o,t}}}\\
&=\delta_{o,t}\\\
\frac{\partial{E}}{\partial{\mathbf{b}_{f,t}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{f,t}}}\frac{\partial{\mathbf{net}_{f,t}}}{\partial{\mathbf{b}_{f,t}}}\\
&=\delta_{f,t}\\\
\frac{\partial{E}}{\partial{\mathbf{b}_{i,t}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{i,t}}}\frac{\partial{\mathbf{net}_{i,t}}}{\partial{\mathbf{b}_{i,t}}}\\
&=\delta_{i,t}\\\
\frac{\partial{E}}{\partial{\mathbf{b}_{c,t}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{\tilde{c},t}}}\frac{\partial{\mathbf{net}_{\tilde{c},t}}}{\partial{\mathbf{b}_{c,t}}}\\
&=\delta_{\tilde{c},t}\\
\end{align}
$$
以下是最终的偏置项梯度,即将各个时刻的偏置项梯度加在一起:
$$
\begin{align}
\frac{\partial{E}}{\partial{\mathbf{b}_o}}&=\sum_{j=1}^t\delta_{o,j}\\
\frac{\partial{E}}{\partial{\mathbf{b}_i}}&=\sum_{j=1}^t\delta_{i,j}\\
\frac{\partial{E}}{\partial{\mathbf{b}_f}}&=\sum_{j=1}^t\delta_{f,j}\\
\frac{\partial{E}}{\partial{\mathbf{b}_c}}&=\sum_{j=1}^t\delta_{\tilde{c},j}\\
\end{align}
$$
对于\(W_{fx},W_{ix},W_{cx},W_{ox}\)的权重梯度,只需要根据相应的误差项直接计算即可:
$$
\begin{align}
\frac{\partial{E}}{\partial{W_{ox}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{o,t}}}\frac{\partial{\mathbf{net}_{o,t}}}{\partial{W_{ox}}}\\
&=\delta_{o,t}\mathbf{x}_{t}^T\\\
\frac{\partial{E}}{\partial{W_{fx}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{f,t}}}\frac{\partial{\mathbf{net}_{f,t}}}{\partial{W_{fx}}}\\
&=\delta_{f,t}\mathbf{x}_{t}^T\\\
\frac{\partial{E}}{\partial{W_{ix}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{i,t}}}\frac{\partial{\mathbf{net}_{i,t}}}{\partial{W_{ix}}}\\
&=\delta_{i,t}\mathbf{x}_{t}^T\\\
\frac{\partial{E}}{\partial{W_{cx}}}&=\frac{\partial{E}}{\partial{\mathbf{net}_{\tilde{c},t}}}\frac{\partial{\mathbf{net}_{\tilde{c},t}}}{\partial{W_{cx}}}\\
&=\delta_{\tilde{c},t}\mathbf{x}_{t}^T\\
\end{align}
$$
一般现实中使用的LSTM还将output和hidden进行拼接,如下图:
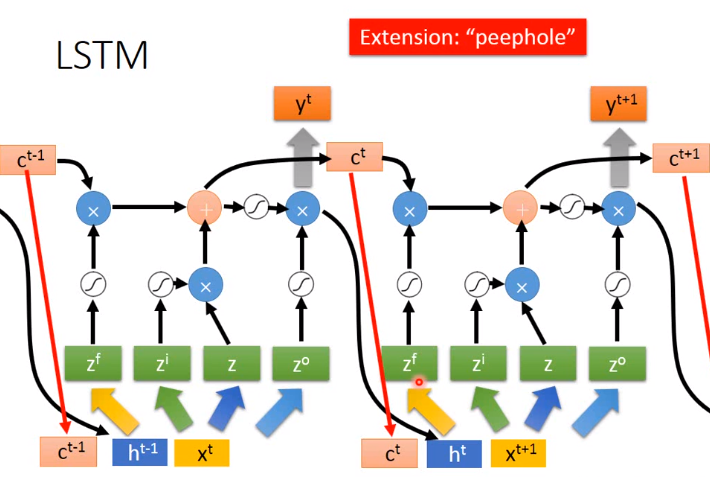
GRU
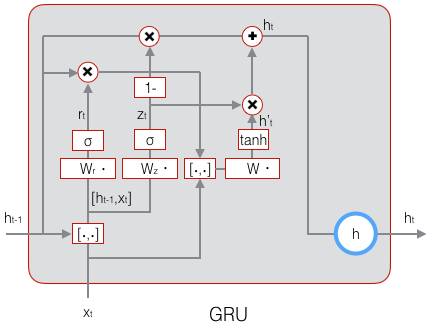
GRU (Gated Recurrent Unit)是众多LSTM变体中的最成功的一种,它对LSTM做了很多简化,同时还保持着和LSTM相同的效果。
GRU对LSTM做了两个大改动:
- 将输入门、遗忘门、输出门变为两个门:更新门(Update Gate)\(z_t\)和重置门(Reset Gate)\(r_t\)。
- 将单元状态与输出合并为一个状态: \(h\)
GRU的前向计算公式为:
$$
\begin{align}
\mathbf{z}_t&=\sigma(W_z\cdot[\mathbf{h}_{t-1},\mathbf{x}_t])\\
\mathbf{r}_t&=\sigma(W_r\cdot[\mathbf{h}_{t-1},\mathbf{x}_t])\\
\mathbf{\tilde{h}}_t&=\tanh(W\cdot[\mathbf{r}_t\circ\mathbf{h}_{t-1},\mathbf{x}_t])\\
\mathbf{h}&=(1-\mathbf{z}_t)\circ\mathbf{h}_{t-1}+\mathbf{z}_t\circ\mathbf{\tilde{h}}_t
\end{align}
$$
下图是GRU的示意图:
本文主要参考了零基础入门深度学习-长短时记忆网络LSTM,更加强烈推荐大家去看台大李弘毅老师的例子LSTM实例
RNN的应用
- 在slot filling的问题中,RNN的输入和输出相同的长度
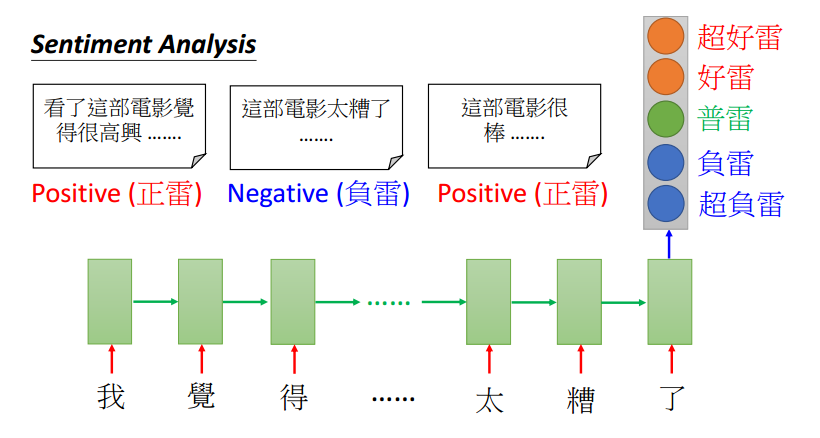
- LSTM的输入可以是一个向量序列,输出可以只是一个向量,一般用于情感分析,如下图:
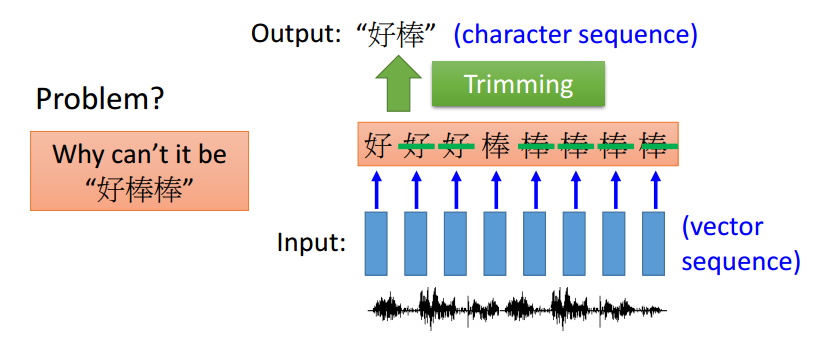
- LSTM的输入和输出也可以是序列,并且输出序列可以更短,一般用于语音识别,如下图:
- LSTM的输入和输出都可以是序列,并且长度可以不一,一般可以用于机器翻译,如下图:
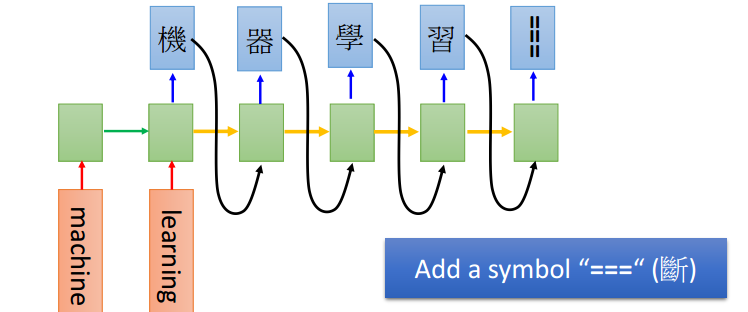
- LSTM也可以只需要一个输入,但是输出可以是序列,如下图:
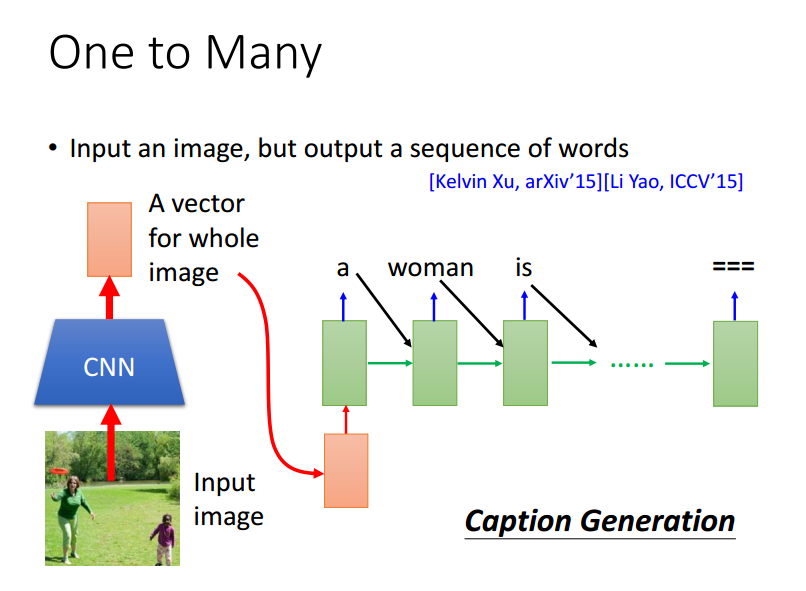
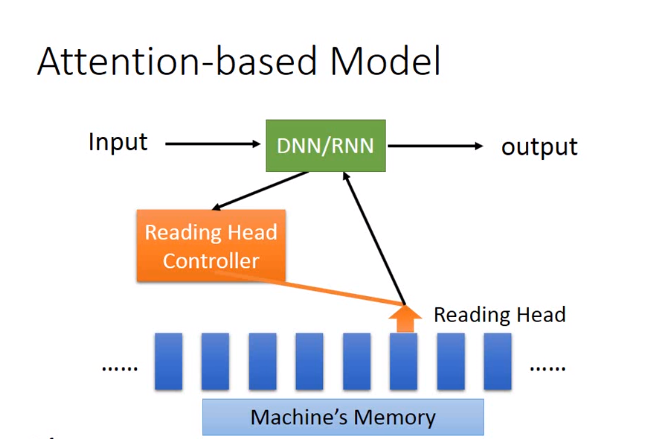
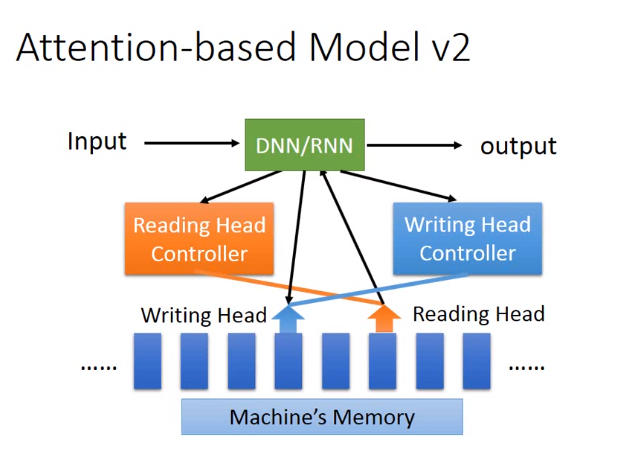
Attention-based Model