RNN 循环神经网络
RNN 基本概念
RNN就是将隐藏层的输出存储到内存中,和下一次的input一起输入,所以会有一定的记忆性。
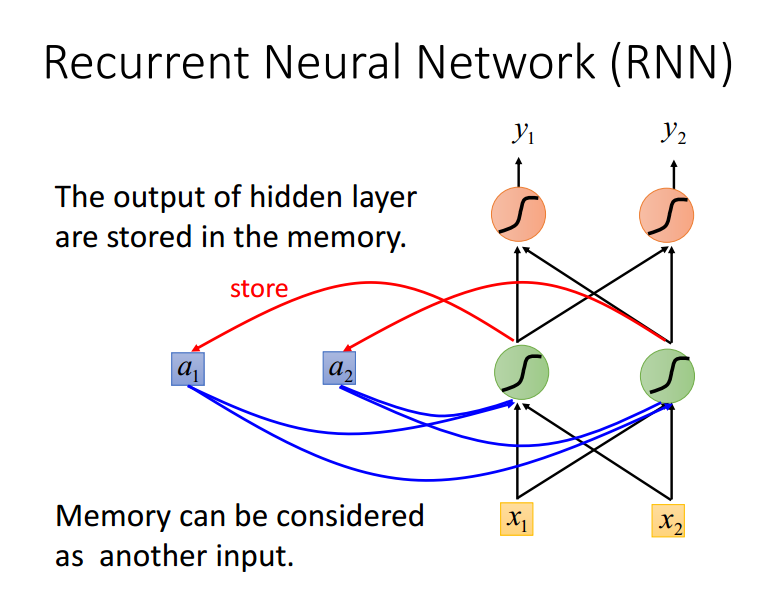
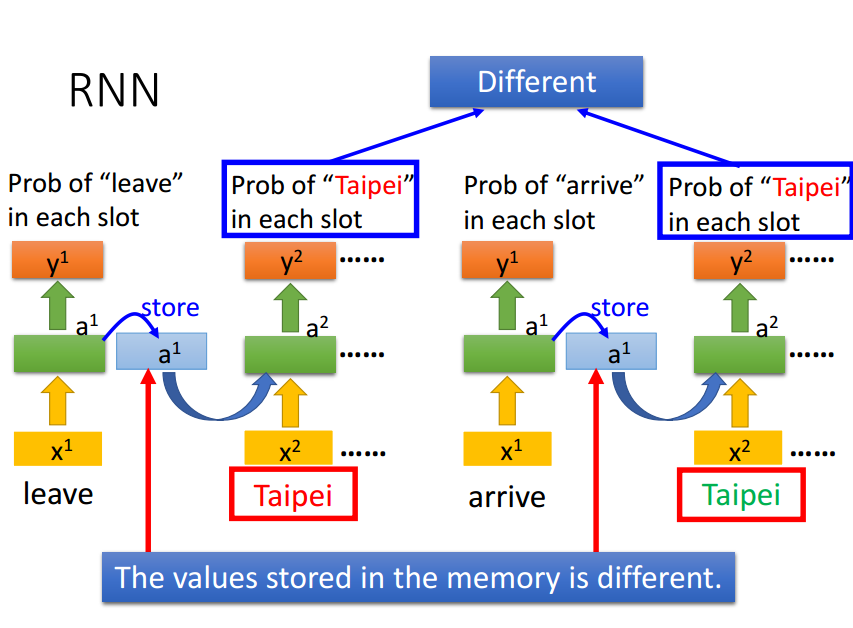
RNN并不是将一句话直接输入,而是将一句话的所有的词一个一个以词向量的形式输入到网络中。
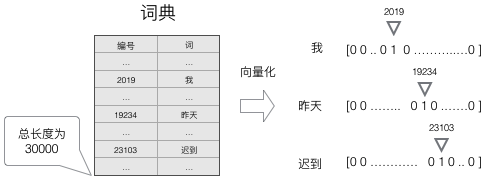
更加直观的如下显示,一般得到高维、稀疏的向量,针对高维稀疏的向量会带来庞大的计算量,因此,往往会使用一些降维方法,将高维的稀疏向量转变为低维的稠密向量
语言模型要求的输出是下一个最可能的词,我们可以让循环神经网络计算计算词典中每个词是下一个词的概率,这样,概率最大的词就是下一个最可能的词。因此,神经网络的输出向量也是一个N维向量,向量中的每个元素对应着词典中相应的词是下一个词的概率。如下图所示:
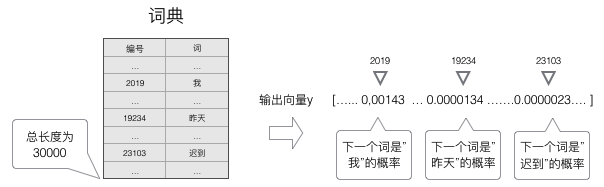
若让神经网络输出概率,那么就是让softmax层作为网络的输出层
RNN的缺陷就是无法处理长距离依赖问题且输入与输出维度相同
上文主要是参考台大李弘毅老师的ppt
RNN 训练算法推导
BPTT是针对循环层的训练方法,基本原理与BP算法一样,包括了三个步骤:
- 前向计算每个神经元的输出值
- 反向计算每个神经元的误差项\(\delta_{j}\),它是损失函数E对神经元\(j\)的加权输入\(net_{j}\)的偏导数,即上一篇BP算法推导中的\(\delta_{j} = \frac{\partial E}{\partial net_{j}}\),其中,\(\frac{\partial E}{\partial w} = \frac{\partial E}{\partial net_{j}}\frac{\partial net_{j}}{\partial w} \),即\(\frac{\partial E}{\partial w} = \delta_{j}\frac{\partial net_{j}}{\partial w} \)
- 计算每个权重的梯度
- 使用随机梯度下降算法(SGD)更新权重
循环层如下图所示:
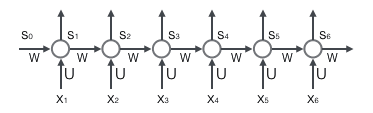
前向计算
前向计算的公式很简单,根据上图有如下公式,向量的下标\(t\)表示时刻。
$$s_{t} = f(Ux_{t}+Ws_{t-1})$$
反向计算误差项
在BPTT将第l层t时刻的误差值\(\delta_t^l\)沿两个方向传播:
- 一个方向是其传递到上一层网络,从上图上来看是最底层,得到\(\delta_t^{l-1}\),这部分只与权值矩阵\(U\)有关
- 另一个方向是将其沿时间线传递到初始时刻,得到\(\delta_1^l\),这部分只和权值矩阵\(w\)有关。
时间轴方向
用向量\(net_{t}\)表示神经元在t时刻的输入
$$
\begin{align}
\mathrm{net}_t&=U\mathrm{x}_t+W\mathrm{s}_{t-1}
\end{align}
$$
$$
\begin{align}
\mathrm{s}_{t-1}&=f(\mathrm{net}_{t-1})
\end{align}
$$
所以:
$$
\begin{align}
\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_{t-1}}}&=\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{s}_{t-1}}}\frac{\partial{\mathrm{s}_{t-1}}}{\partial{\mathrm{net}_{t-1}}}
\end{align}
$$
其中第一项结果为Jacobian矩阵:
$$
\begin{align}
\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{s}_{t-1}}}&=
\begin{bmatrix}
\frac{\partial{net_1^t}}{\partial{s_1^{t-1}}}& \frac{\partial{net_1^t}}{\partial{s_2^{t-1}}}& …& \frac{\partial{net_1^t}}{\partial{s_n^{t-1}}}\\
\frac{\partial{net_2^t}}{\partial{s_1^{t-1}}}& \frac{\partial{net_2^t}}{\partial{s_2^{t-1}}}& …& \frac{\partial{net_2^t}}{\partial{s_n^{t-1}}}\\
&.\\&.\\
\frac{\partial{net_n^t}}{\partial{s_1^{t-1}}}& \frac{\partial{net_n^t}}{\partial{s_2^{t-1}}}& …& \frac{\partial{net_n^t}}{\partial{s_n^{t-1}}}\
\end{bmatrix}
&=\begin{bmatrix}
w_{11} & w_{12} & … & w_{1n}\\
w_{21} & w_{22} & … & w_{2n}\\
&.\\&.\\
w_{n1} & w_{n2} & … & w_{nn}\
\end{bmatrix}
&=W
\end{align}
$$
同理,第二项也是一个Jacobian矩阵:
$$
\begin{align}
\frac{\partial{\mathrm{s}_{t-1}}}{\partial{\mathrm{net}_{t-1}}}&=
\begin{bmatrix}
\frac{\partial{s_1^{t-1}}}{\partial{net_1^{t-1}}}& \frac{\partial{s_1^{t-1}}}{\partial{net_2^{t-1}}}& …& \frac{\partial{s_1^{t-1}}}{\partial{net_n^{t-1}}}\\
\frac{\partial{s_2^{t-1}}}{\partial{net_1^{t-1}}}& \frac{\partial{s_2^{t-1}}}{\partial{net_2^{t-1}}}& …& \frac{\partial{s_2^{t-1}}}{\partial{net_n^{t-1}}}\\
&.\\&.\\
\frac{\partial{s_n^{t-1}}}{\partial{net_1^{t-1}}}& \frac{\partial{s_n^{t-1}}}{\partial{net_2^{t-1}}}& …& \frac{\partial{s_n^{t-1}}}{\partial{net_n^{t-1}}}
\end{bmatrix}\\
&=\begin{bmatrix}
f’(net_1^{t-1}) & 0 & … & 0\\
0 & f’(net_2^{t-1}) & … & 0\\
&.\\&.\\
0 & 0 & … & f’(net_n^{t-1})\\
\end{bmatrix}\\
&=diag[f’(\mathrm{net}_{t-1})]
\end{align}
$$
最后两项合在一起可得:
$$
\begin{align}
\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_{t-1}}}&=\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{s}_{t-1}}}\frac{\partial{\mathrm{s}_{t-1}}}{\partial{\mathrm{net}_{t-1}}}\\
&=Wdiag[f’(\mathrm{net}_{t-1})]\\
&=\begin{bmatrix}
w_{11}f’(net_1^{t-1}) & w_{12}f’(net_2^{t-1}) & … & w_{1n}f(net_n^{t-1})\\
w_{21}f’(net_1^{t-1}) & w_{22} f’(net_2^{t-1}) & … & w_{2n}f(net_n^{t-1})\\
&.\\&.\\
w_{n1}f’(net_1^{t-1}) & w_{n2} f’(net_2^{t-1}) & … & w_{nn} f’(net_n^{t-1})\\
\end{bmatrix}
\end{align}
$$
至此,在时间轴方向,可以求得任意时刻k的误差项\(\delta_k\)
$$
\begin{align}
\delta_k^T=&\frac{\partial{E}}{\partial{\mathrm{net}_k}}\\
=&\frac{\partial{E}}{\partial{\mathrm{net}_t}}\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_k}}\\
=&\frac{\partial{E}}{\partial{\mathrm{net}_t}}\frac{\partial{\mathrm{net}_t}}{\partial{\mathrm{net}_{t-1}}}\frac{\partial{\mathrm{net}_{t-1}}}{\partial{\mathrm{net}_{t-2}}}…\frac{\partial{\mathrm{net}_{k+1}}}{\partial{\mathrm{net}_{k}}}\\
=&Wdiag[f’(\mathrm{net}_{t-1})]
Wdiag[f’(\mathrm{net}_{t-2})]
…
Wdiag[f’(\mathrm{net}_{k})]
\delta_t^T\\
=&\delta_t^T\prod_{i=k}^{t-1}Wdiag[f’(\mathrm{net}_{i})]\qquad
\end{align}
$$
传递到上一层方向
该层与普通的全连接层完全一样,循环层的加权输入\(net^l\)与上一层的加权输入\(net^{l-1}\)关系如下,式子中\(\mathrm{net}_t^l\)是第l层神经元的加权输入(假设第l层是循环层),\(\mathrm{net}_t^{l-1}\)是第l-1层神经元的加权输入,\(\mathrm{a}_t^{l-1}\)是第l-1层神经元的输出,\(\mathrm{f}^{l-1}\)是第l-1层的激活函数
$$
\begin{align}
\mathrm{net}_t^l=&U\mathrm{a}_t^{l-1}+W\mathrm{s}_{t-1}\\
\mathrm{a}_t^{l-1}=&f^{l-1}(\mathrm{net}_t^{l-1})
\end{align}
$$
与时间轴方向函数类似,求得:
$$
\begin{align}
\frac{\partial{\mathrm{net}_t^l}}{\partial{\mathrm{net}_t^{l-1}}}=&\frac{\partial{\mathrm{net}^l}}{\partial{\mathrm{a}_t^{l-1}}}\frac{\partial{\mathrm{a}_t^{l-1}}}{\partial{\mathrm{net}_t^{l-1}}}\\
=&Udiag[f’^{l-1}(\mathrm{net}_t^{l-1})]
\end{align}
$$
$$
\begin{align}
(\delta_t^{l-1})^T=&\frac{\partial{E}}{\partial{\mathrm{net}_t^{l-1}}}\\
=&\frac{\partial{E}}{\partial{\mathrm{net}_t^l}}\frac{\partial{\mathrm{net}_t^l}}{\partial{\mathrm{net}_t^{l-1}}}\\
=&(\delta_t^l)^TUdiag[f’^{l-1}(\mathrm{net}_t^{l-1})]\qquad
\end{align}
$$
权重的梯度的计算
计算误差函数E对权重梯度W的梯度函数如下:
$$ \frac{\partial{E}}{\partial{W}} $$
对该梯度函数进行计算:
$$
\begin{align}
\mathrm{net}_t=&U\mathrm{x}_t+W\mathrm{s}_{t-1}\\
\begin{bmatrix}
net_1^t\\
net_2^t\\
.\\.\\
net_n^t\\
\end{bmatrix}=&U\mathrm{x}_t+
\begin{bmatrix}
w_{11} & w_{12} & … & w_{1n}\\
w_{21} & w_{22} & … & w_{2n}\\
.\\.\\
w_{n1} & w_{n2} & … & w_{nn}\\
\end{bmatrix}
\begin{bmatrix}
s_1^{t-1}\\
s_2^{t-1}\\
.\\.\\
s_n^{t-1}\\
\end{bmatrix}\\
=&U\mathrm{x}_t+
\begin{bmatrix}
w_{11}s_1^{t-1}+w_{12}s_2^{t-1}…w_{1n}s_n^{t-1}\\
w_{21}s_1^{t-1}+w_{22}s_2^{t-1}…w_{2n}s_n^{t-1}\\
.\\.\\
w_{n1}s_1^{t-1}+w_{n2}s_2^{t-1}…w_{nn}s_n^{t-1}\\
\end{bmatrix}
\end{align}
$$
由于\(w_{ji}\)只与\(net_j^t\)有关,所以:
$$
\begin{align}
\frac{\partial{E}}{\partial{w_{ji}}}=&\frac{\partial{E}}{\partial{net_j^t}}\frac{\partial{net_j^t}}{\partial{w_{ji}}}\\
=&\delta_j^ts_i^{t-1}
\end{align}
$$
最终的梯度\(\frac{\partial{E}}{\partial{W}}\)是各个时刻的w的梯度之和
$$
\begin{align}
\frac{\partial{E}}{\partial{W}}=&\sum_{i=1}^t\frac{\partial{E}}{\partial{W_i}}\\
=&\begin{bmatrix}
\delta_1^ts_1^{t-1} & \delta_1^ts_2^{t-1} & … & \delta_1^ts_n^{t-1}\\
\delta_2^ts_1^{t-1} & \delta_2^ts_2^{t-1} & … & \delta_2^ts_n^{t-1}\\
.\\.\\
\delta_n^ts_1^{t-1} & \delta_n^ts_2^{t-1} & … & \delta_n^ts_n^{t-1}\\
\end{bmatrix}
+…+
\begin{bmatrix}
\delta_1^1s_1^0 & \delta_1^1s_2^0 & … & \delta_1^1s_n^0\\
\delta_2^1s_1^0 & \delta_2^1s_2^0 & … & \delta_2^1s_n^0\\
.\\.\\
\delta_n^1s_1^0 & \delta_n^1s_2^0 & … & \delta_n^1s_n^0\\
\end{bmatrix}\qquad
\end{align}
$$
同权重矩阵W类似,我们可以得到权重矩阵U的计算方法。
$$
\frac{\partial{E}}{\partial{U_t}}=\begin{bmatrix}
\delta_1^tx_1^t & \delta_1^tx_2^t & … & \delta_1^tx_m^t\\
\delta_2^tx_1^t & \delta_2^tx_2^t & … & \delta_2^tx_m^t\\
.\\.\\
\delta_n^tx_1^t & \delta_n^tx_2^t & … & \delta_n^tx_m^t
\end{bmatrix}\qquad
$$
上式是误差函数在t时刻对权重矩阵U的梯度。和权重矩阵W一样,最终的梯度也是各个时刻的梯度之和:
$$ \frac{\partial{E}}{\partial{U}}=\sum_{i=1}^t\frac{\partial{E}}{\partial{U_i}} $$
RNN缺点
即w在不同的时间点被反复的使用,所以较难训练
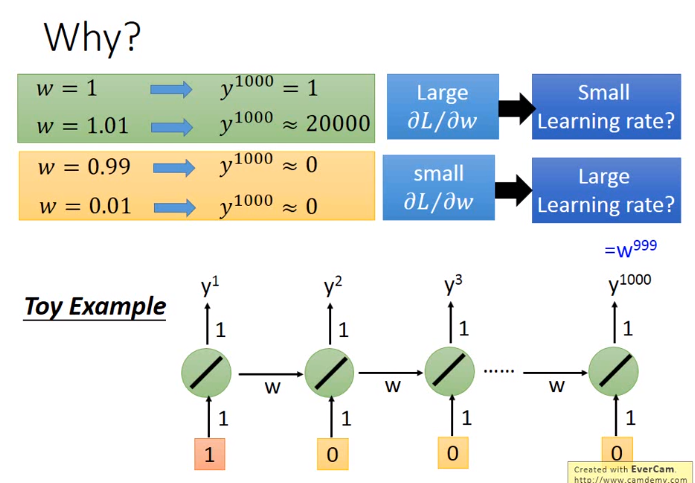
解决方式:
- LSTM,LSTM可以解决RNN中的gradient vanishing的问题。(不是gradient explode的问题)为什么?因为RNN中的memory每次会被覆盖且只来自于上一次的memory,而LSTM的memory是原先的memory与input相加得来。LSTM里的memory除非forget gate关闭,否则之前的memory的值的影响不会消失