梯度下降法
损失函数是关于输入权重和偏置的二次函数(使用平方差),分别对权重和偏置求偏导数,即梯度向量。
沿着梯度向量的方向是训练误差(损失函数)增长最快的地方,而沿着梯度向量相反的方向,梯度减少最快,在这个方向上更容易找到训练误差(损失函数)的最小值
BP算法
- 隐藏层和输出层均使用sigmoid函数
$$o(x) = \frac{1}{1+e^{-x}}$$
- sigmoid函数求导:
$$\frac{\partial (o(x)) }{\partial x} = o(x)(1-o(x))$$
- 损失函数\(E\)使用平方差
$$E=\frac{1}{2}\sum_{k\in outputs}^{ }(y_{k}-o_{k})^{2}$$
- 推导的网络层数为3层,如下所示,其中\(y_{k}\)表示输出层第\(k\)个神经元标签值,\(o_{k}\)表示第\(k\)个神经元的输出,\(net_{k}\)表示没有经过激活函数之前的输出,即\(net_{k} = \sum_{j=0}^{n}w_{jk}*\sigma (net_j)\)
由于是从网上复制的图片,实则输出层输出符号应改为\(o_{1}\)…\(o_{k}\)
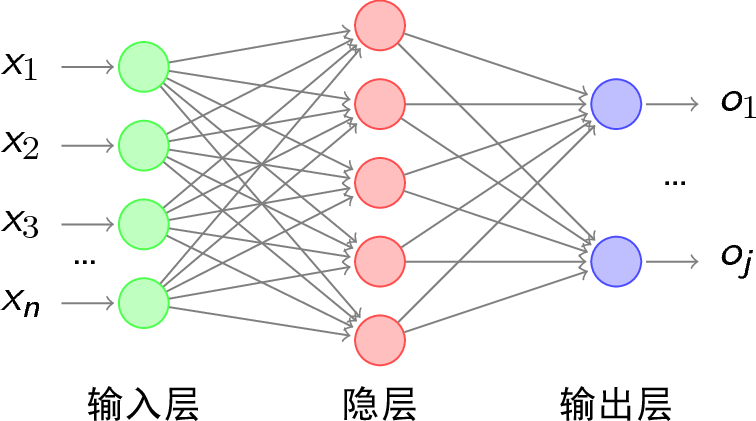
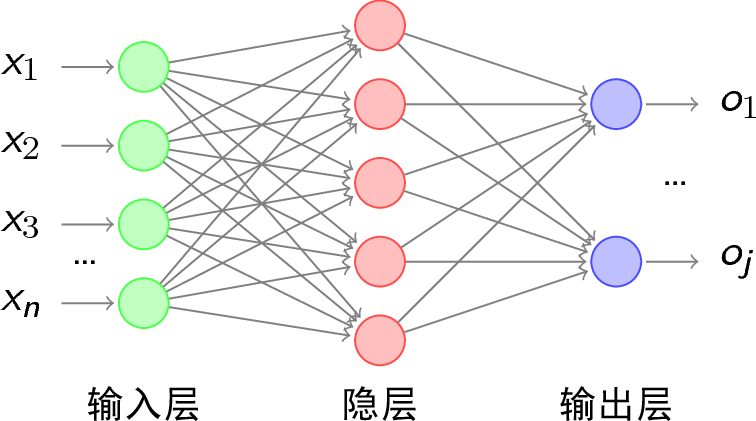
其中
- \(net_{j} = \sum_{i=0}^{n}w_{ij}*x_{ij}\)
- \(net_{k} = \sum_{j=0}^{n}w_{jk}*\sigma (net_j)\)
BP算法主要更新层与层之间的权值\(w_{ij}\)
对于只有一个样本就进行梯度下降计算的随机梯度下降算法(SGD),权值更新公式如下:
$$w_{ij}=w_{ij}+\Delta w$$
对于有m个样本时,就是把每一个的效果累加起来再除以m:
$$w_{ij}=w_{ij}+\frac{1}{m}\sum_{z=1}^{z=m}\Delta w$$
对于网络中的每个权值\(w_{jk}\),计算其导数为:
$$\frac{\partial E}{\partial w_{jk}} = \frac{\partial E}{\partial net_{k}}\frac{\partial net_{k}}{\partial w_{jk}} = \frac{\partial E}{\partial net_{k}}\frac{\partial (\sum_{j=0}^{n}w_{jk}x_{jk})}{\partial w_{jk}} = \frac{\partial E}{\partial net_{k}}x_{jk}$$
其中\(x_{jk} = \sigma(net_{j})\)
1. 若k为输出层单元
对\(net_{k}\)的求导:
$$\frac{\partial E}{\partial net_{k}} = \frac{\partial E}{\partial o_{k}}\frac{\partial o_{k}}{\partial net_{k}}$$
其中,\(\sigma ()\)为sigmoid激活函数:
$$\frac{\partial E}{\partial o_{k}} = \frac{\partial (\frac{1}{2}\sum_{k\in outputs,k=i}^{ }(y_{k}-o_{k})^2)}{\partial o_{k}} = -(y_{k}-o_{k})$$
$$\frac{\partial o_{k}}{\partial net_{k}} = \frac{\partial (\sigma (net_{k}))}{\partial net_{k}} = o_{k}(1-o_{k})$$
所以有:
$$\frac{\partial E}{\partial net_{k}} = \frac{\partial E}{\partial o_{k}}\frac{\partial o_{k}}{\partial net_{k}} = -(y_{k}-o_{k})o_{k}(1-o_{k})$$
为了表达更加简洁,我们使用:
$$\delta _ {k} = - \frac{\partial E}{\partial net_{k}} = (y_{k}-o_{k})o_{k}(1-o_{k})$$
权值的改变沿着损失函数的梯度反方向,\(\eta\)为学习率
$$\Delta w_{jk} = -\eta \frac{\partial E}{\partial w_{jk}} = -\eta \frac{\partial E}{\partial net_k}x_{jk}=-\eta [ -(y_{k}-o_{k})o_{k}(1-o_{k}) ]x_{jk}$$
其中\(x_{jk} = \sigma(net_{j})\)
2. 若j是隐藏层的单元
对于隐藏层单元\(j\),输入层到隐藏层的权值\(w_{ij}\)跟所有的从隐藏层到输出层的权值\(w_{jk}\)有关,对于输入层到隐藏层的权值\(w_{ij}\),计算其导数。
其中
- \(net_{j} = \sum_{i=0}^{n}w_{ij}*x_{ij}\)
- \(net_{k} = \sum_{j=0}^{n}w_{jk}*\sigma (net_j)\)
$$\frac{\partial E}{\partial w_{ij}} = \frac{\partial E}{\partial net_{j}}\frac{\partial net_{j}}{\partial w_{ij}} = \frac{\partial E}{\partial net_{j}}\frac{\partial (\sum_{i=0}^{n}w_{ij}x_{ij})}{\partial w_{ij}} = \frac{\partial E}{\partial net_{j}}x_{ij}$$
$$\frac{\partial E}{\partial net_{j}} = \sum_{k\in outputs}^{ }\frac{\partial E}{\partial net_{k}}\frac{\partial net_{k}}{\partial net_{j}}$$
又因为由1中推导的公式可得:
$$\delta _ {k} = - \frac{\partial E}{\partial net_{k}}$$
所以:
$$\frac{\partial E}{\partial net_{j}} = \sum_{k\in outputs}^{ }-\delta _{k}\frac{\partial net_{k}}{\partial net_{j}} = \sum_{k\in outputs }^{ }-\delta _{k}\frac{\partial net_{k}}{\partial \sigma _{j}}\frac{\partial \sigma _{j}}{\partial net_{j}}$$
因为:
$$\frac{\partial net_{k}}{\partial \sigma _{j}} = \frac{\partial (\sum_{j\in hidden,k\in outputs}^{ } w_{jk}\sigma_{j})} {\partial \sigma_{j}} = w_{jk}$$
$$\frac{\partial \sigma _{{j}}}{\partial net_{j}} = o_{j}(1-o_{j})$$
所以:
$$\frac{\partial E}{\partial net_{j}} = \sum_{k\in outputs }^{ }-\delta _{k}\frac{\partial net_{k}}{\partial \sigma _{{j}}}\frac{\partial \sigma _{{j}}}{\partial net_{j}} = \sum_{k\in outputs }^{ }-\delta _{k}w_{jk}o_{j}(1-o_{j})$$
同样,我们使用:
$$\delta _{j} = - \frac{\partial E}{\partial net_{j}} = o_{j}(1-o_{j})\sum_{k\in outputs }^{ }\delta _{k}w_{jk} $$
权值的改变沿着损失函数的梯度反方向,\(\eta\)为学习率
$$\Delta w_{ij} = -\eta \frac{\partial E}{\partial w_{ij}} = -\eta \frac{\partial E}{\partial net_j}x_{ij}$$
BP算法的改进
1.增加冲量项
让第n次迭代时的权值更新部分依赖于第n-1次的权值
原因:
- 加入冲量项在一定程度上起到加大搜索步长的效果,从而能更快的收敛
- 加入冲量项之后可以越过某些局部极小值,达到更小的地方
$$\Delta w_{ij}(n) = \eta \delta _{j} x_{ij} + \alpha \Delta w_{ij}(n-1) $$
对于多个隐藏层求\(\Delta w_{ij}\)
因为:
$$\Delta w_{ij} = -\eta \frac{\partial E}{\partial w_{ij}} = -\eta \frac{\partial E}{\partial net_j}x_{xj} = \eta \delta _{j}x_{ij}$$
所以,第k层的误差由更深的第k+1层的误差计算得到:
$$\delta _{j} = o_{j}(1-o_{j})\sum_{k\in j+1 layer }^{ }\delta _{k}w_{jk} $$
